贝叶斯概率视角下的市场周期预测新解

撰文：NingNing

截至2025年，我们完整经历不到4轮四年周期。然而，统计学常识提醒我们，在极小样本规模（有效数据仅3个）下得出任何结论都需要谨慎验证，而非简单迷信。

在小样本的大市场周期预测中，基于贝叶斯概率方法推导出2025年第四季度对标2019年第四季度的刻学分析，比传统的四年周期论更具参考价值。

将2025年第四季度对标2019年第四季度的刻学转换为贝叶斯公式表达：

P（熊市｜美林时钟滞涨衰退）=[P( 熊市）/P（美林时钟滞涨衰退）]*（P（美林时钟滞涨衰退｜熊市）

贝叶斯概率参数估算

P( 熊市 ) - 先验概率

自1929年以来：S&P 500经历了27次熊市

平均频率：每3.5年一次

年度概率：约28.6%

季度概率（Q4-Q1跨度）：约15-20%

保守估计：P( 熊市 ) ≈ 18%

P( 滞涨→衰退 ) - 美林时钟转换概率

历史上「滞涨→衰退」的转换概率：

1970年代滞涨：最终导致1973-74、1980、1981-82三次衰退

2000-2001：科技泡沫破裂，温和衰退

2007-2008：金融危机，深度衰退

2011-2012：欧债危机，未完全衰退（避免）

2018-2019：贸易战担忧，软着陆成功

统计估算：

过去50年约6次「滞涨→衰退」情景

其中4次转为衰退（66%）

2次软着陆（34%）

当前环境调整：

美联储主动降息（vs 1970s被动加息）

劳动力市场韧性（vs 2008金融系统性风险）

关税政策不确定性

全球去美元化压力

估计：P( 滞涨→衰退 ) ≈ 40-50%（取中值45%）

P( 滞涨→衰退|熊市 ) - 似然概率

在熊市发生的条件下，经历「滞涨→衰退」的概率：

历史熊市分类：

衰退型熊市（12次）：1929、1937、1973-74、1980、1981-82、1990、2000-02、2007-09、2020、2022

非衰退型熊市（15次）：其他技术性调整

在12次衰退型熊市中：

经历滞涨阶段的：1973-74、1980、1981-82、2007-08（约4次）

未经历滞涨的：1929（通缩）、2020（疫情冲击）、2022（纯通胀）

估计：P( 滞涨→衰退|熊市 ) ≈ 33%

贝叶斯计算

标准公式：

P( 熊市|滞涨→衰退 ) = P( 滞涨→衰退|熊市 ) × P( 熊市 ) / P( 滞涨→衰退 )

= 0.33 × 0.18 / 0.45

= 0.0594 / 0.45

= 0.132 = 13.2%

情景分析矩阵

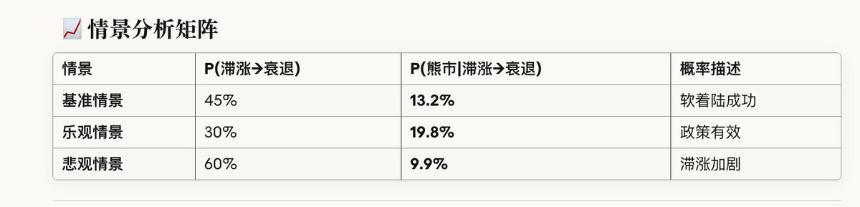
关键差异分析：为何概率较低？

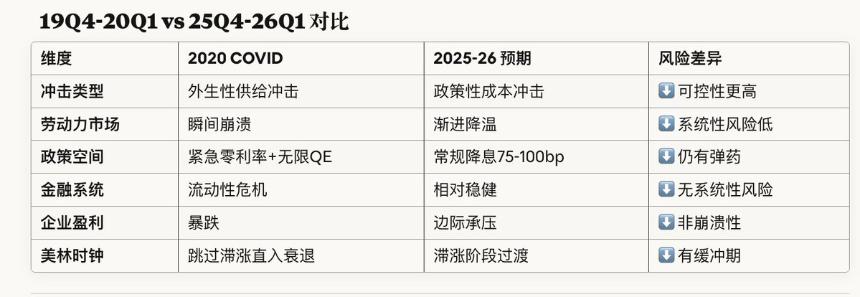
综合结论

P(2025Q4-2026Q1 熊市 ) ≈ 15-20%

置信区间：

下限（乐观）：12%

中值（基准）：17%

上限（悲观）：25%

策略

需要战术性防御而非战略性撤退。